This is a method driven by the same constraints as the exponential moving average, but for median and other percentiles.
We present an algorithm for tracking the value of a percentile, such as the median, in an infinite stream of observations whose distribution can change over time. A self-imposed constraint is that we cannot afford to keep the last N observations explicitly in memory. In our algorithm, the cost of updating the estimated percentile is \(O(1)\) and the memory usage is also \(O(1)\). A single parameter denoted \(r\) is specified by the user and expresses the trade-off between accuracy and reactivity (to changes in the distribution of the signal).
Notations: in this document, all sequences and arrays are indexed starting from 0.
Given N a fixed window length, it is relatively straightforward to maintain a sorted array \(W\) of the latest N observations indexed \(0\dots N-1\). The p-percentile is computed exactly over that window by looking up the pair of values found at index \(\lfloor (N-1)p \rfloor\) and at index \(\lceil (N-1)p \rceil\), and by taking their average.
For example, the median \(m\) (0.5-percentile) using a window of length \(N=100\) is calculated as follows once we’ve read 100 observations or more:
\[m = \frac{W_{49} + W_{50}}{2}\]
Such algorithms are not acceptable for us since they require storing the latest N values, where N is typically chosen greater than 100.
An exponential moving average is a weighted average of the previous observations, in which the weight of the latest observation is always set to a fixed parameter \(r\) (\(0 \lt r \le 1\)) and the weight of the other values is \((1-r)\) times their previous weight.
After reading \(\lfloor 1/r \rfloor + 1\) observations or more, the moving average for observation i is computed as follows:
\[m_i = r . x_i + (1-r) . m_{i-1}\]
In the initial phase where \(i \lt \lfloor 1/r \rfloor\), \(m_i\) is calculated as the mean of all the observations so far. The rationale is that the weight of the latest observation is the nearest possible to \(r\) without being smaller than the weight any of the past observations. This avoids having to set \(m_{-1}\) to an arbitrary guess with a lasting impact. Updating m in this initial phase is done as follows:
\[\hat{r}_i = \frac{1}{i+1}\] \[m_i = \hat{r}_i . x_i + (1-\hat{r}_i) . m_{i-1}\]
This exponential moving average algorithm is used in the moving percentile algorithm described below to estimate the standard deviation of the signal.
The \(p\)-percentile is represented by the variable \(m\). It is initialized with the value of the first observation \(x_0\):
\[ m_0 = x_0 \]
Subsequent iterations are updated as follows, for some value of \(\delta\) discussed later.
If \(x_i < m_{i-1}\) then
\[ m_i = m_{i-1} - \frac{\delta}{p} \]
else if \(x_i > m_{i-1}\) then
\[ m_i = m_{i-1} + \frac{\delta}{1-p} \]
else \(x_i = m_{i-1}\) and keep the previous value:
\[ m_i = m_{i-1} \]
If \(\delta\) is not too large and not too small, \(m\) is a good estimate of the \(p\)-percentile. Choosing a good value for \(\delta\) depends on the distribution of values around the \(p\)-percentile. Excessive values of \(\delta\) result in big jumps for m and limit the accuracy, while a \(\delta\) that’s too small may take too much time to converge to the \(p\)-percentile as computed exactly using a window of a reasonable length.
In order to express the trade-off between accuracy and convergence speed, we express \(\delta\) as the product of a user-chosen constant r and the estimated standard deviation \(\sigma\) of the input signal:
\[ \delta_i = \sigma_i . r \]
where \(\sigma_i\) is the square root of the variance estimated by a moving average of the sequence \((\mu_i - x_i)^2\) and \(\mu\) is estimated by a moving average of x.
We find that reasonable values of \(r\) for many applications range from 0.001 to 0.01.
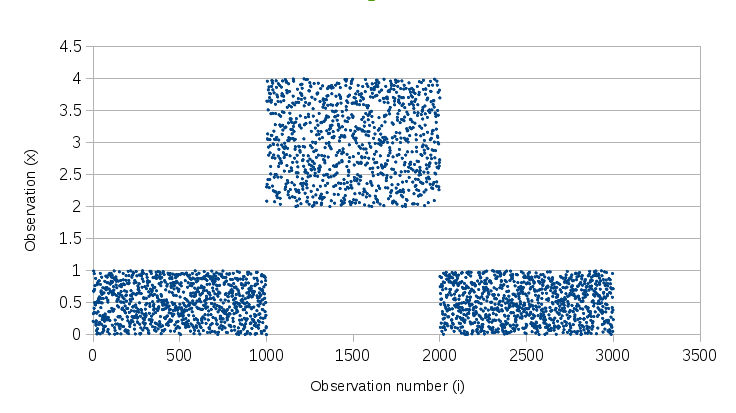
The chart below shows our sample signal that was generated randomly in 3 phases:
The output for window-based percentile estimators and for our moving percentile are shown here:
Our moving 0.9-percentile, shown on the chart in green, reacts quickly when the signal shifts upward, because each update shifts the moving percentile upward by \(\frac{\delta}{0.1}\). However, when the signal shifts downward, it takes the moving percentile more time to react because each update shifts it downward by \(\frac{\delta}{0.9}\), which is 9 times less than in the other direction. Additionally, we can see that the downward shift is pretty steep initially and then gets less steep. This is due to the delayed update of the standard deviation \(\sigma\): the value of \(\delta\) is divided by two when the estimated \(\sigma\) catches up and is divided by two, reflecting the new distribution in phase 3.
A sample implementation is available on GitHub.